経験分布の収束について

概要

ブートストラップ法を勉強していて，経験分布に関して興味が湧いた点があったので個人的に整理する．

具体的には，経験分布関数が元の分布関数へ大数の法則より収束することと，類似に定義できる経験密度関数がヒストグラムと対応でき，こちらも概ね(？)元の分布の密度関数へ収束することを示したい(願望)．

この記事において，経験分布関数の定義と\text{indicator function}の扱いあたりは、概ねこの本の１章に基づく．

経験分布の定義と各種グラフ

簡単のため，以下で扱う分布関数Fは微分可能であり，密度関数\frac{dF(x)}{dx}=f(x)が存在すると仮定する．

まず，IIDで分布関数Fに従うN個の確率変数を\boldsymbol{X}=\{X_1, X_2, \cdots , X_N\}，その実現値を\boldsymbol{x}=\{x_1, x_2, \cdots, x_N\}とする．
ここでFに関する経験分布関数\hat{F}は次のように定義される．

\displaystyle \hat{F}(z) = \frac{1}{N} \sum_{i=1}^N I_{A_z} (x_i)

ただし，A_z = \{y| y \in \mathbb{R}, y \leq z\}，I_S(x)は次のように定義される\text{indicator function}である．

I_S (x)= \begin{cases} 1 & \text{if } x \in S \\ 0 & \text{otherwise} \end{cases}

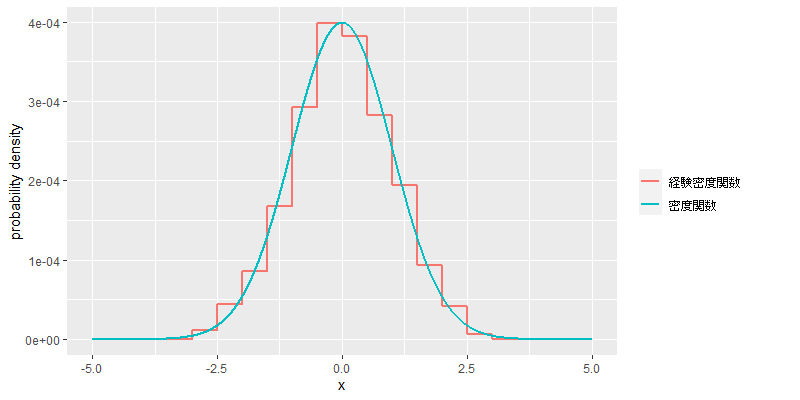
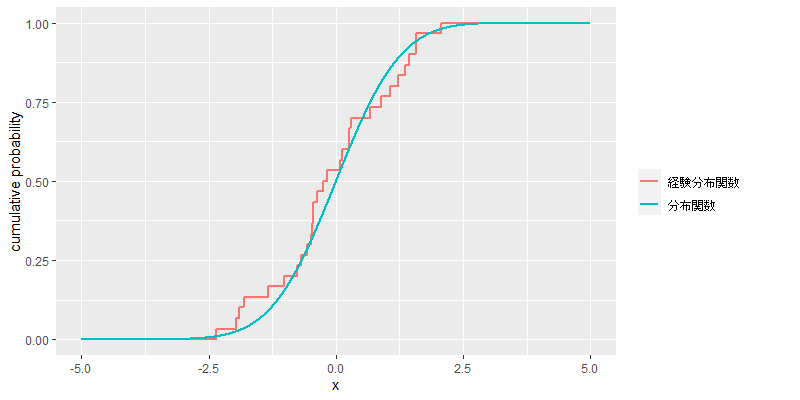
次に例示として，標準正規分布における分布関数と，N=30の標本に基づく経験分布関数のグラフを示す．

f:id:JosephBell:20210204220016p:plain
分布関数と経験分布関数


ある区間サイズ\Deltaについて，経験密度関数を次のように定義する．

\displaystyle \hat{f}(z) = \frac{1}{\Delta} \frac{1}{N} \sum_{i=1}^N I_{B_z} (x_i)

ただし，B_z = \{y | y \in \mathbb{R}, c_z \leq y \leq c_z + \Delta\}，c_z = \Delta \lfloor z / \Delta \rfloorとする．ここで \lfloor x \rfloorは床関数である．
（注：ここでの経験密度関数は，ヒストグラムと密度関数の対応を見るために導入したこの記事独自のものである）

次に例示として，標準正規分布おける密度関数と，N=1000の標本に基づく経験密度関数のグラフを示す（\Delta=0.5）．

f:id:JosephBell:20210205222111p:plain
密度関数と経験密度関数

経験分布関数のFへの収束

N \rightarrow \inftyのとき，大数の法則により\hat{F}(z)はE_F[I_{A_z}(X)]へ確率収束する．

\displaystyle \hat{F}(z) = \frac{1}{N} \sum_{i=1}^N I_{A_z}(x_i) \overset{p}{\rightarrow} E_F [I_{A_z} (X)] ~ \text{ as } ~ N \rightarrow \infty


そして次のようにE[I_{A_z}(X)]はF(z)へ帰着される．

\displaystyle E[I_{A_z}(X)] = \int_{- \infty}^{\infty} I_{A_z} (x) dF(x) = \int_{- \infty}^{z} dF(x) = F(z)


以上ように，経験分布関数\hat{F}は分布関数Fへ漸近的に収束する．


経験密度関数のfへの収束

経験分布関数の場合と同様に，N \rightarrow \inftyのとき，大数の法則により\hat{f}(z)は\frac{1}{\Delta} E_F[I_{B_z}(X)]へ確率収束する．

\displaystyle \hat{f}(z) = \frac{1}{\Delta} \frac{1}{N} \sum_{i=1}^N I_{B_z}(x_i) \overset{p}{\rightarrow} \frac{1}{\Delta} E_F [I_{B_z} (X)] ~ \text{ as } ~ N \rightarrow \infty


ここから\frac{1}{\Delta} E_F[I_{B_z}(X)]は，次のようにF(c_z)に関するニュートン商に帰着される．

\displaystyle \begin{align} \frac{1}{\Delta} E[I_{B_z}(X)] &= \frac{1}{\Delta} \int_{- \infty}^{\infty} I_{B_z} (x) dF(x) = \frac{1}{ \Delta} \int_{c_z}^{c_z + \Delta} dF(x) \\ &= \frac{1}{\Delta} \left\{ \int_{- \infty}^{c_z + \Delta} dF(x) - \int_{- \infty}^{c_z} dF(x) \right\} \\ &= \frac{ F(c_z + \Delta) - F(c_z) }{\Delta} \end{align}


次に \displaystyle \lim_{\Delta \to 0} c_z = zを示す．
まず \lfloor z / \Delta \rfloorに明らかに成り立つ関係を考え，それに\Deltaをかける．

\displaystyle \frac{z}{\Delta} - 1 < \lfloor z/ \Delta \rfloor \leq \frac{z}{\Delta} \Leftrightarrow z - \Delta < \Delta \lfloor z / \Delta \rfloor \leq z

ここで\displaystyle \lim_{\Delta \to 0} \{ z - \Delta \} = zであるから，はさみうちの原理から次のように目的の極限は示される．

\displaystyle \lim_{\Delta \to 0} c_z = \lim_{\Delta \to 0} \Delta \lfloor z / \Delta \rfloor = z


最終的に\frac{1}{\Delta} E_F[I_{B_z}(X)]は \Delta \to 0のとき，f(z)に帰着される．

\displaystyle \lim_{\Delta \to 0} \frac{1}{\Delta} E_F[I_{B_z}(X)] = \lim_{\Delta \to 0} \frac{ F(c_z + \Delta) - F(c_z) }{\Delta} = \frac{dF(z)}{dz} = f(z)


以上ように，経験密度関数\hat{f}は漸近的な収束先において， \Delta \to 0となるとき，密度関数fに収束する．
最終的な極限に関しては，ニュートン商とc_zが同時に収束しているところを曖昧に扱っているので，正直なところ自信がない．その辺りの曖昧な部分に問題があるとわかったらまた修正する．