読書：『意識はどこから生まれてくるのか』(マーク・ソームズ)

意識に関する書籍は、ジュリオ・トノーニの『意識はいつ生まれるのか』以来、とても久しぶり読んだ。
本書マーク・ソームズの『意識はどこから生まれてくるのか』は、概して大変興味深く、いくつかの点で自分が漠然と持っていた意識と脳に対する認識は大幅に変わった。

特に本書前半の議論(第1～6章)、意識は認識的というよりも感情的(あるいは「感じ」)で、脳における意識の座は大脳皮質ではなく、脳幹上部であるという主張は、実際に脳に障害を受けた人の症例を多く扱い、個人的には説得力があった。
また、心理学における行動主義以降、徹底して軽んじられていた内観報告の役割を重視した神経心理学研究、著者が神経精神分析学と呼ぶもの、も新鮮で面白かった。

フロイトが元々しっかりとした神経生理学者で、当時の神経生理学的な技術的限界から精神分析学を興したことはどこかで読んで知っていたが、将来的な技術発展を見据えたプロジェクトまで構想していたことは、本書を読むまで知らなかった。
著者はフロイトが当時挫折せざるを得なかった、このプロジェクトを現代に蘇らせたらしいので、時間があったら少し読んでみたい。


しかしながら、自由エネルギー原理が出てくるあたり(第7章)は個人的には微妙だった。
すでに一冊自由エネルギー原理に関する本は読んだことがあるが、やはりなんというかFEPは腑に落ちない。
本書にの説明においても、結局のところ予測誤差を最小化する(FEP的には自由エネルギーを最小化する)ことが生命にとって重要で原理であると、端的に言えば述べているだけで、そこまで劇的なものとは思えない(ホメオスタシス的なネガティブフィードバックシステムに関しても、雰囲気、制御工学的システムを情報理論の観点から捉えなおして、適応範囲を広げた以上のことではない気がしている)。
情報系の自分には、物理学関連の用語と概念が多用されているのでハードルは高いが、そのうちFEPに関してはちゃんと時間をとって学ぶ必要があるかもしれない…

また、フリストンが構築したらしい自己組織化システムと、そこでの重要概念と捉えられているマルコフブランケットあたりの議論は、正直オートポイエーシスや人工生命分野で散々やられてきたことの焼き直しなのではないかという気がするし、神経系が実現する自己組織系と、単細胞レベルで実現される自己組織化系ではギャップが大きすぎて、著者の主張にそこまで乗れなかった。差分として敷衍されている自己組織系の内部における外部のFEP的な予測の話が、なにかこれまでにない凄いことなのかもしれないが、これも判断がつかなかった。


第11章の「意識のハードプロブレム」は期待していたが、チャーマーズの元々の論文を縦軸に議論する形で、恐らくあと1～2回読み直しても理解度は7割を超えない気がしている。大枠雰囲気で理解した範囲では、チャーマーズのハードプロブレムの議論には、概念の混合があり、根本的にハードプロブレムではないという話に帰着しようとしているように見受けられるが、正直この辺りはチャーマーズの原論文と適当な副読本を含め、しっかり読まないとついていけないと感じた。

第12章の「心を作る」では、本書での知見を用いて実際に意識を持った機械を作る具体的な方法について論じているが、その試みの構想は大変ナイーブに感じた。実際に人工生命研究とかを行った経験のある人なら多かれ少なかれ理解されると思うが、これこれこういうステップで目的の生命的な振る舞いや認知をシミュレートするという研究は、試行錯誤の連続で、ほとんど最初の構想通りにはいかない(個人的経験)。
とはいえ、本書通してこの著者は、1つならず、多くの大胆な発想や主張を行ってきており、何か面白い結果が得られる可能性は期待している。

経験分布の収束について

概要

ブートストラップ法を勉強していて，経験分布に関して興味が湧いた点があったので個人的に整理する．

具体的には，経験分布関数が元の分布関数へ大数の法則より収束することと，類似に定義できる経験密度関数がヒストグラムと対応でき，こちらも概ね(？)元の分布の密度関数へ収束することを示したい(願望)．

この記事において，経験分布関数の定義と\text{indicator function}の扱いあたりは、概ねこの本の１章に基づく．

経験分布の定義と各種グラフ

簡単のため，以下で扱う分布関数Fは微分可能であり，密度関数\frac{dF(x)}{dx}=f(x)が存在すると仮定する．

まず，IIDで分布関数Fに従うN個の確率変数を\boldsymbol{X}=\{X_1, X_2, \cdots , X_N\}，その実現値を\boldsymbol{x}=\{x_1, x_2, \cdots, x_N\}とする．
ここでFに関する経験分布関数\hat{F}は次のように定義される．

\displaystyle \hat{F}(z) = \frac{1}{N} \sum_{i=1}^N I_{A_z} (x_i)

ただし，A_z = \{y| y \in \mathbb{R}, y \leq z\}，I_S(x)は次のように定義される\text{indicator function}である．

I_S (x)= \begin{cases} 1 & \text{if } x \in S \\ 0 & \text{otherwise} \end{cases}

次に例示として，標準正規分布における分布関数と，N=30の標本に基づく経験分布関数のグラフを示す．

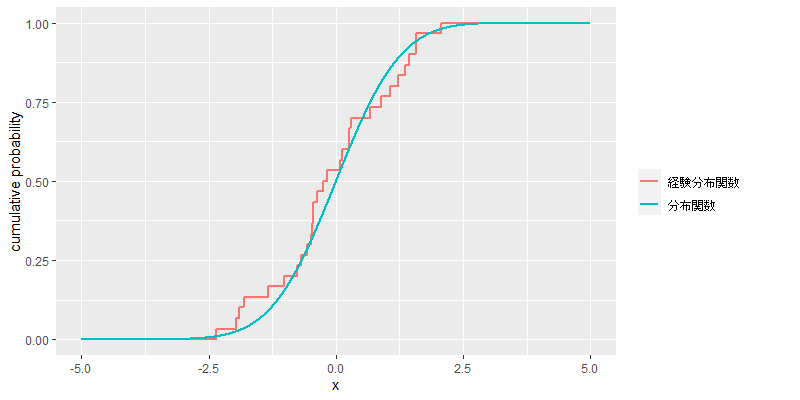
f:id:JosephBell:20210204220016p:plain
分布関数と経験分布関数


ある区間サイズ\Deltaについて，経験密度関数を次のように定義する．

\displaystyle \hat{f}(z) = \frac{1}{\Delta} \frac{1}{N} \sum_{i=1}^N I_{B_z} (x_i)

ただし，B_z = \{y | y \in \mathbb{R}, c_z \leq y \leq c_z + \Delta\}，c_z = \Delta \lfloor z / \Delta \rfloorとする．ここで \lfloor x \rfloorは床関数である．
（注：ここでの経験密度関数は，ヒストグラムと密度関数の対応を見るために導入したこの記事独自のものである）

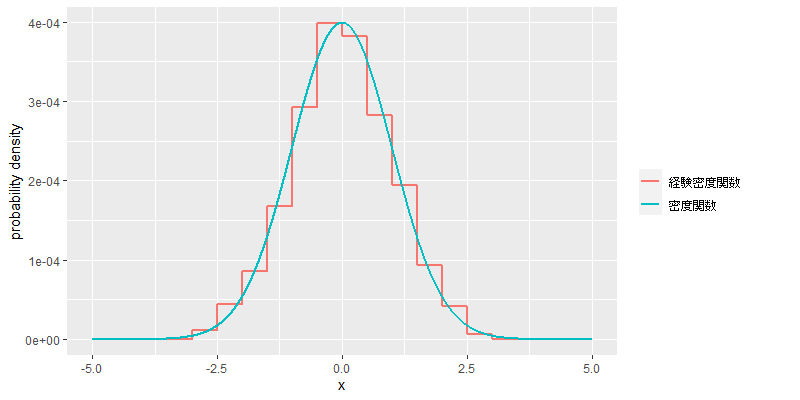
次に例示として，標準正規分布おける密度関数と，N=1000の標本に基づく経験密度関数のグラフを示す（\Delta=0.5）．

f:id:JosephBell:20210205222111p:plain
密度関数と経験密度関数

経験分布関数のFへの収束

N \rightarrow \inftyのとき，大数の法則により\hat{F}(z)はE_F[I_{A_z}(X)]へ確率収束する．

\displaystyle \hat{F}(z) = \frac{1}{N} \sum_{i=1}^N I_{A_z}(x_i) \overset{p}{\rightarrow} E_F [I_{A_z} (X)] ~ \text{ as } ~ N \rightarrow \infty


そして次のようにE[I_{A_z}(X)]はF(z)へ帰着される．

\displaystyle E[I_{A_z}(X)] = \int_{- \infty}^{\infty} I_{A_z} (x) dF(x) = \int_{- \infty}^{z} dF(x) = F(z)


以上ように，経験分布関数\hat{F}は分布関数Fへ漸近的に収束する．


経験密度関数のfへの収束

経験分布関数の場合と同様に，N \rightarrow \inftyのとき，大数の法則により\hat{f}(z)は\frac{1}{\Delta} E_F[I_{B_z}(X)]へ確率収束する．

\displaystyle \hat{f}(z) = \frac{1}{\Delta} \frac{1}{N} \sum_{i=1}^N I_{B_z}(x_i) \overset{p}{\rightarrow} \frac{1}{\Delta} E_F [I_{B_z} (X)] ~ \text{ as } ~ N \rightarrow \infty


ここから\frac{1}{\Delta} E_F[I_{B_z}(X)]は，次のようにF(c_z)に関するニュートン商に帰着される．

\displaystyle \begin{align} \frac{1}{\Delta} E[I_{B_z}(X)] &= \frac{1}{\Delta} \int_{- \infty}^{\infty} I_{B_z} (x) dF(x) = \frac{1}{ \Delta} \int_{c_z}^{c_z + \Delta} dF(x) \\ &= \frac{1}{\Delta} \left\{ \int_{- \infty}^{c_z + \Delta} dF(x) - \int_{- \infty}^{c_z} dF(x) \right\} \\ &= \frac{ F(c_z + \Delta) - F(c_z) }{\Delta} \end{align}


次に \displaystyle \lim_{\Delta \to 0} c_z = zを示す．
まず \lfloor z / \Delta \rfloorに明らかに成り立つ関係を考え，それに\Deltaをかける．

\displaystyle \frac{z}{\Delta} - 1 < \lfloor z/ \Delta \rfloor \leq \frac{z}{\Delta} \Leftrightarrow z - \Delta < \Delta \lfloor z / \Delta \rfloor \leq z

ここで\displaystyle \lim_{\Delta \to 0} \{ z - \Delta \} = zであるから，はさみうちの原理から次のように目的の極限は示される．

\displaystyle \lim_{\Delta \to 0} c_z = \lim_{\Delta \to 0} \Delta \lfloor z / \Delta \rfloor = z


最終的に\frac{1}{\Delta} E_F[I_{B_z}(X)]は \Delta \to 0のとき，f(z)に帰着される．

\displaystyle \lim_{\Delta \to 0} \frac{1}{\Delta} E_F[I_{B_z}(X)] = \lim_{\Delta \to 0} \frac{ F(c_z + \Delta) - F(c_z) }{\Delta} = \frac{dF(z)}{dz} = f(z)


以上ように，経験密度関数\hat{f}は漸近的な収束先において， \Delta \to 0となるとき，密度関数fに収束する．
最終的な極限に関しては，ニュートン商とc_zが同時に収束しているところを曖昧に扱っているので，正直なところ自信がない．その辺りの曖昧な部分に問題があるとわかったらまた修正する．

AICの背景からのAICcの導出

このブログでは，下記記事のAICの導出における背景を踏襲してAICcの導出を行う．

josephbell.hatenablog.com

主要参考文献は下記の3つである．

  1. Cavanaugh and Neath (2018)
  2. Konishi and Kitagawa (2008)
  3. Hurvich and Tsai (1989)

AICの背景に追加の前提

AICの導出では，モデルの取る分布はパラメトリックなクラスに属するという仮定しか置いていなかったが，AICcの導出においては，モデルの取る具体的な構造を正規線形モデルに限定する．

\displaystyle \boldsymbol{Y}_n = X\boldsymbol{\beta} + \boldsymbol{\epsilon}, ~~~~~ \boldsymbol{\epsilon} \sim N_n (\boldsymbol{0}, {\sigma}^2 I_n )

ここでXはn\times mの計画行列，\boldsymbol{\beta}はm次元のパラメタベクタ，I_nはn \times nの単位行列である．
このモデル設定において，真のモデルは平均をX_0 \boldsymbol{\beta}_0，分散共分散行列を{{\sigma}_0}^2 I_nとするn次元の多変量正規分布である；ここでX_0の列数と\boldsymbol{\beta}_0の次元は未知であることに留意する．

尤度関数は具体的に次のように定まる．

\displaystyle \begin{align} L(\boldsymbol{\theta}_k | \boldsymbol{y}_n) &= \prod_{i=1}^n f(y_i | \boldsymbol{\theta}_k) = \prod_{i = 1}^n (2 \pi {\sigma}^2)^{- \frac{1}{2}} \text{exp} \left\{ - \frac{ (y_i - {\boldsymbol{x}_i}^T \boldsymbol{\beta} )^2 }{ 2 {\sigma}^2 } \right\} \\ &= (2 \pi {\sigma}^2)^{- \frac{n}{2}} \text{exp} \left\{ - \frac{1}{2 {\sigma}^2} \sum_{i=1}^n (y_i - {\boldsymbol{x}_i}^T \boldsymbol{\beta} )^2 \right\} \\ &= (2 \pi {\sigma}^2)^{- \frac{n}{2}} \text{exp} \left\{ - \frac{(\boldsymbol{y}_n - X \boldsymbol{\beta} )^T (\boldsymbol{y}_n - X \boldsymbol{\beta} )}{2 {\sigma}^2} \right\}\end{align}

k=m+1とおき，このモデルにおける最尤推定量\hat{\boldsymbol{\theta}}_{k} = (\hat{\boldsymbol{\beta}}^T, \hat{\sigma}^2)^T (\in \Theta(k))は次のように求まる．

\displaystyle \hat{\boldsymbol{\beta}} = (X^T X)^{-1} X^T \boldsymbol{Y}_n
\displaystyle \hat{\sigma}^2 = \frac{1}{n} (\boldsymbol{Y}_n - X \hat{\boldsymbol{\beta}})^T (\boldsymbol{Y}_n - X \hat{\boldsymbol{\beta}})

n個の観測に関するカルバック不一致は次のような形になる．

\displaystyle \begin{align} d_n(\boldsymbol{\theta}_{k}) &= E \{ -2 \text{log} f(\boldsymbol{Y}_n | \boldsymbol{\theta}_{k}) \} \\ &= -2 E \left\{ \text{log} \left[ (2 \pi {\sigma}^2)^{- \frac{n}{2}} \text{exp} \left\{ - \frac{(\boldsymbol{Y}_n - X \boldsymbol{\beta} )^T (\boldsymbol{Y}_n - X \boldsymbol{\beta} )}{2 {\sigma}^2} \right\} \right] \right\} \\ &= n \text{log} (2 \pi {\sigma}^2) + \frac{1}{{\sigma}^2} E \left\{ (X_0 \boldsymbol{\beta}_0 + \boldsymbol{\epsilon} - X \boldsymbol{\beta} )^T (X_0 \boldsymbol{\beta}_0 + \boldsymbol{\epsilon} - X \boldsymbol{\beta} ) \right\} \\ &= n \text{log} (2 \pi {\sigma}^2) +\frac{n {{\sigma}_0}^2}{ {\sigma}^2 } + \frac{ (X_0 \boldsymbol{\beta}_0 - X \boldsymbol{\beta} )^T (X_0 \boldsymbol{\beta}_0 - X \boldsymbol{\beta} ) }{ {\sigma}^2 } \end{align}

d_n(\boldsymbol{\theta}_{k})は次に示すようにn倍した1個の観測に関するカルバック不一致n d(\boldsymbol{\theta}_{k})と等価であることに留意する．

\displaystyle \begin{align} d_n(\boldsymbol{\theta}_{k}) &= E \{ -2 \text{log} f(\boldsymbol{Y}_n | \boldsymbol{\theta}_{k}) \} \\ &= \int g(\boldsymbol{y}_n) \{ -2 \text{log} f(\boldsymbol{y}_n | \boldsymbol{\theta}_{k}) \} d\boldsymbol{y}_n = \sum_{i=1}^n \int g(\boldsymbol{y}_n) \{ -2 \text{log} f(y_i|\boldsymbol{\theta}_{k}) \} d\boldsymbol{y}_n \\ &= \sum_{i=1}^n \int \cdots \int g(y_1) \cdots g(y_n) \{ -2 \text{log} f(y_i|\boldsymbol{\theta}_{k}) \} dy_1 \cdots dy_n \\ &= \sum_{i=1}^n \left\{ \int g(y_i) \{ -2 \text{log} f(y_i|\boldsymbol{\theta}_{k}) \} dy_i \prod_{j \in S_i} \int g(y_j) dy_j \right\} \\ &= \sum_{i=1}^n \int g(y_i) \{ -2 \text{log} f(y_i|\boldsymbol{\theta}_{k}) \} dy_i = \sum_{i=1}^n E \{ -2 \text{log} f(Y | \boldsymbol{\theta}_{k}) \} = n d(\boldsymbol{\theta}_{k}) \end{align}

ここで S_i = \{s| s \in \mathbb{N}, s \neq i, 1 \leq s \leq n\}である．

AICcの導出

追加された前提も含め，n個の観測に関する期待カルバック不一致を求める．

\displaystyle \begin{align} \Delta_n (k) &= E \{ d_n (\hat{\boldsymbol{\theta}}_{k}) \} \\ &= E \left\{ n \text{log} (2 \pi \hat{\sigma}^2) + \frac { n {{\sigma}_0}^2}{ \hat{\sigma}^2 } + \frac{ (X_0 \boldsymbol{\beta}_0 - X \hat{\boldsymbol{\beta}} )^T (X_0 \boldsymbol{\beta}_0 - X \hat{\boldsymbol{\beta}} ) }{ \hat{\sigma}^2 } \right\} \\ &= E \left\{ n \text{log} (2 \pi \hat{\sigma}^2) \right\} + E \left\{ \frac { n {{\sigma}_0}^2}{ \hat{\sigma}^2 } \right\} + E \left\{ \frac{ (X_0 \boldsymbol{\beta}_0 - X \hat{\boldsymbol{\beta}} )^T (X_0 \boldsymbol{\beta}_0 - X \hat{\boldsymbol{\beta}} ) }{ \hat{\sigma}^2 } \right\} \end{align}


まず，(SSE/{{\sigma}_0}^2) \sim {\chi}^2 (n - m)であり(Puntanen et al. (2013))，\hat{\sigma}^2の定義からSSE = n \hat{\sigma}^2であることから，n \hat{\sigma}^2 / {{\sigma}_0}^2は{\chi}^2 (n - m)に従い， {{\sigma}_0}^2 / (n \hat{\sigma}^2)は \text{Inv-}{\chi}^2 (n - m)に従う(Hamada et al. 2008)．このことから \Delta_n(k)の第2項は次のように求まる．

\displaystyle E \left\{ \frac{ n \hat{\sigma}^2 }{ {{\sigma}_0}^2 } \right\} = n^2 E \left\{ \frac{ \hat{\sigma}^2 }{ n {{\sigma}_0}^2 } \right\} = \frac{ n^2 }{ n - m - 2 }


次に，候補モデルのクラス\mathcal{F}(k)に真の分布g(y)が含まれているという強い仮定を置く．この仮定の下では，X_0 = Xかつ，\boldsymbol{\beta}_0は未知のm次元パラメタベクタである；仮定により \Delta_n(k)の第3項は次のように変形できる．

\displaystyle E \left\{ \frac{ (X_0 \boldsymbol{\beta}_0 - X \hat{\boldsymbol{\beta}} )^T (X_0 \boldsymbol{\beta}_0 - X \hat{\boldsymbol{\beta}} ) }{ \hat{\sigma}^2 } \right\} = E \left\{ \frac{ ( \hat{\boldsymbol{\beta}} - \boldsymbol{\beta}_0 )^T X^T X (\hat{\boldsymbol{\beta}} - \boldsymbol{\beta}_0 ) }{ \hat{\sigma}^2 } \right\}

正規線形モデルにおいて，最尤推定量である回帰係数は誤差\boldsymbol{\epsilon}の線形変換と等価であり， \hat{\boldsymbol{\beta}} - \boldsymbol{\beta}_0は多変量正規分布 N_m (\boldsymbol{0}, {{\sigma}_0}^2 \{ X^T X \}^{-1} )に従うことから(Madisen and Thyregod (2010), p.49, Theorem 3.3)， \Delta_n(k)の第3項の期待値内は次のようにF分布に帰着できる．

\displaystyle \frac{ ( \hat{\boldsymbol{\beta}} - \boldsymbol{\beta}_0 )^T X^T X (\hat{\boldsymbol{\beta}} - \boldsymbol{\beta}_0 ) }{ \hat{\sigma}^2 } = \frac{nm}{n-m} \frac{ (( \hat{\boldsymbol{\beta}} - \boldsymbol{\beta}_0 )^T X^T X(\hat{\boldsymbol{\beta}} - \boldsymbol{\beta}_0 ) / {{\sigma}_0}^2) (1/m) }{ (n \hat{\sigma}^2 / {{\sigma}_0}^2) ( 1 / (n - m) ) }

\displaystyle \Rightarrow \frac{n-m}{nm} \frac{ ( \hat{\boldsymbol{\beta}} - \boldsymbol{\beta}_0 )^T X^T X (\hat{\boldsymbol{\beta}} - \boldsymbol{\beta}_0 ) }{ \hat{\sigma}^2 } = \frac{ (( \hat{\boldsymbol{\beta}} - \boldsymbol{\beta}_0 )^T X^T X(\hat{\boldsymbol{\beta}} - \boldsymbol{\beta}_0 ) / {{\sigma}_0}^2) (1/m) }{ (n \hat{\sigma}^2 / {{\sigma}_0}^2) ( 1 / (n - m) ) } \sim F(m, n-m)

ゆえに

\displaystyle \begin{align} E \left\{ \frac{ ( \hat{\boldsymbol{\beta}} - \boldsymbol{\beta}_0 )^T X^T X (\hat{\boldsymbol{\beta}} - \boldsymbol{\beta}_0 ) }{ \hat{\sigma}^2 } \right\} &= \frac{nm}{n-m} E \left\{ \frac{n-m}{nm} \frac{ ( \hat{\boldsymbol{\beta}} - \boldsymbol{\beta}_0 )^T X^T X (\hat{\boldsymbol{\beta}} - \boldsymbol{\beta}_0 ) }{ \hat{\sigma}^2 } \right\} \\ &= \frac{nm}{n-m} E \left\{ \frac{ (( \hat{\boldsymbol{\beta}} - \boldsymbol{\beta}_0 )^T X^T X(\hat{\boldsymbol{\beta}} - \boldsymbol{\beta}_0 ) / {{\sigma}_0}^2) (1/m) }{ (n \hat{\sigma}^2 / {{\sigma}_0}^2) ( 1 / (n - m) ) } \right\} \\ &= \frac{nm}{n-m} \frac{n-m}{n-m-2} = \frac{nm}{n-m-2} \end{align}



最終的に全体としてまとめると \Delta_n (k)は次のようになる．

\displaystyle \begin{align} \Delta_n (k) &= E \{ n \text{log} (2 \pi \hat{\sigma}^2) \} + \frac{ n^2 }{ n - m - 2 } + \frac{nm}{n-m-2} \\ &= E \{ n (\text{log} (2 \pi \hat{\sigma}^2) + 1) \} + \frac{2n(m + 1)}{n-m-2} \end{align}

ここで n (\text{log} (2 \pi \hat{\sigma}^2) + 1)は-2倍した最大対数尤度であることに留意する．

\displaystyle \begin{align} -2 \text{log} f (\boldsymbol{Y}_n|\hat{\boldsymbol{\theta}}_{k}) &= n \text{log} (2 \pi \hat{\sigma}^2 ) + \frac{ (\boldsymbol{Y}_n - X \hat{\boldsymbol{\beta}})^T (\boldsymbol{Y}_n - X \hat{\boldsymbol{\beta}}) }{ \hat{\sigma}^2 } \\ &= n \text{log} (2 \pi \hat{\sigma}^2 ) + \frac{n \hat{\sigma}^2 }{ \hat{\sigma}^2 } = n (\text{log} (2 \pi \hat{\sigma}^2) + 1) \end{align}

ここからAICcは次のように定義される．

\displaystyle \text{AICc} = n (\text{log} (2 \pi \hat{\sigma}^2) + 1) + \frac{2n(m + 1)}{n-m-2} = \text{AIC} + \frac{2 (m + 1)(m + 2)}{n - m - 2}

AICcの期待値は \Delta_n (k)となる．

\displaystyle E \{ \text{AICc} \} = E \{ n (\text{log} (2 \pi \hat{\sigma}^2) + 1) \} + \frac{2n(m + 1)}{n-m-2} = \Delta_n (k)


等価なものとして，AICcはしばしばkを用いても示される．

\displaystyle \text{AICc} = n (\text{log} (2 \pi \hat{\sigma}^2) + 1) + \frac{2nk}{n-k-1} = \text{AIC} + \frac{2k (k + 1)}{n - k - 1}



所感

基本的にはこれまで調べてきたことの組み合わせのつもりで書き始めたブログだったが，n個の観測に関するカルバック不一致は1個の観測に関するものの単純なn倍になることや，正規線形モデルの回帰係数に関する最尤推定量は，誤差に仮定された正規性から直接的に正規分布に従う等，結構と気がつけた未知のことが多く実り多かった．


なにか間違いに気がついたら修正する．

赤池情報量規準の導出

Cavanaugh and Neath (2018)を読んで得た理解のまとめ．
以下の導出の最終的な主張は文献よりも弱く見えるが，これは自分が理解している範囲で正しい結果に留めた結果である．

背景

未知である真の分布g(y)から独立に生成されたn個の観測値\boldsymbol{y}_n = (y_1, y_2, \cdots, y_n)^Tを特徴づける適切なモデルを選択する状況を考える；ここで観測値は独立であるから，同時確率g(\boldsymbol{y}_n) = \prod_{i=1}^n g(y_i)である．

観測値\boldsymbol{y}_nを定式化あるいは説明するモデルを候補モデルと呼ぶ．任意の候補モデルは構造的に確率分布のパラメトリックなクラスに対応し，具体的には，ある候補モデルはk次元パラメータベクタを取る密度関数のクラス\mathcal{F}(k) によって表される．

\displaystyle \mathcal{F}(k) = \{ f(y|\boldsymbol{\theta}_k) | \boldsymbol{\theta}_k \in \Theta (k) \}

ここで\Theta (k)はk次元ベクタで構成されるパラメタ空間である．文献中，k次元ベクタの要素は\text{functionally independent}であると書かれているがなんの事はわからない


L(\boldsymbol{\theta}_k | \boldsymbol{y}_n)は密度関数f(\boldsymbol{y}_n|\boldsymbol{\theta}_k)に対応する尤度関数を表す：L(\boldsymbol{\theta}_k | \boldsymbol{y}_n) = f(\boldsymbol{y}_n|\boldsymbol{\theta}_k)である．\hat{\boldsymbol{\theta}}_kはパラメタ空間\Theta (k)上で尤度L(\boldsymbol{\theta}_k | \boldsymbol{y}_n)を最大化して得られる推定量のベクタを表す．

\displaystyle \hat{\boldsymbol{\theta}}_k = \underset{\boldsymbol{\theta}_k \in \Theta(k)}{\text{argmax}} ~L(\boldsymbol{\theta}_k | \boldsymbol{y}_n)


多様な構造と次元kを持った候補モデルの集まりを考える；最終的な目的としては，この候補モデルの集まりの中から，真の分布g(y)の最も良い近似となるモデルを探すことである．ここでの最も良い近似となるモデルは，理想的にはg(y)の顕著な特徴を捉えつつ，また得られたデータだけでは正確に推定することができないノイズ等の不要な特徴を無視する．


真の分布と候補モデルの乖離の程度を測定し，これを最小化するモデルとしてより良い近似を得ることを考える；この目的のためカルバックライブラ情報量を用いる．g(y)に関するg(y)とf(y|\boldsymbol{\theta}_k)間のカルバックライブラ情報量は次のように定義される．

\displaystyle \begin{align} I(\boldsymbol{\theta}_k) &= \int g(y) \text{log} \left\{ \frac{ g(y) }{ f(y|\boldsymbol{\theta}_k) } \right\} dy \\ &= E \left\{ \text{log} \frac{g(Y)}{f(Y|\boldsymbol{\theta}_k)} \right\} = E \{ \text{log} g(Y) \} + E \{ - \text{log} f(Y|\boldsymbol{\theta}_k) \} \end{align}

I(\boldsymbol{\theta}_k)は厳密には距離関数ではないが，g(y)とf(y|\boldsymbol{\theta}_k)が異なっていれば異なっているほど増加し，その逆も成り立つので，これら密度関数の乖離の程度を測定するのに使用できる．
次にI(\boldsymbol{\theta}_k)の E \{ - \text{log} f(Y|\boldsymbol{\theta}_k) \} に着目して次を定義する．

\displaystyle d(\boldsymbol{\theta}_k) = E \{ -2 \text{log} f(Y|\boldsymbol{\theta}_k) \}

I(\boldsymbol{\theta}_k)のE \{ \text{log} g(Y) \}は定数なので，I(\boldsymbol{\theta}_k)に基づいて行った候補モデルのランク付けは，d(\boldsymbol{\theta}_k)に基づいたランク付けと等価である．ゆえにd(\boldsymbol{\theta}_k)はI(\boldsymbol{\theta}_k)の適切な代替として利用できる．d(\boldsymbol{\theta}_k)をここではカルバック不一致と呼称する．

重要な点として，カルバック不一致は未知である真の分布g(y)に依存しているため，実際にはd(\boldsymbol{\theta}_k)を求めることはできない．


モデル選択のための妥当な規準を得るため，d(\boldsymbol{\theta}_k)の期待値を考え，そしてパラメータとしては最尤推定量\hat{\boldsymbol{\theta}}_kを使用する．

\displaystyle \begin{align} \Delta(k) &= E \{ d(\hat{\boldsymbol{\theta}}_k)\} \\ &=E \{E \{ -2 \text{log} f(Y|\hat{\boldsymbol{\theta}}_k) \}\} = -2 \int g(\boldsymbol{y}_n) \left\{ \int g(y) \text{log} f(y|\hat{\boldsymbol{\theta}}_k(\boldsymbol{y}_n)) dy \right\} d\boldsymbol{y}_n \end{align}

\Delta(k)はしばしば期待カルバック不一致と呼ばれ，カルバック不一致d(\boldsymbol{\theta}_k)と同様に，\Delta(k)も実際には求めることはできない．


導出

赤池情報量規準は\Delta(k)の近似として導出され得る．

次のようにnが大きくなるとき，大数の弱法則から，-2倍した平均最大対数尤度はカルバック不一致の一致推定量である．

\displaystyle -\frac{2}{n} \sum_{i=1}^{n} \text{log} f(Y_i|\hat{\boldsymbol{\theta}}_k) \overset{p}{\rightarrow} E\{ -2 \text{log} f(Y|\hat{\boldsymbol{\theta}}_k) \} ~ \text{ as } ~ n \rightarrow \infty

このことから -2 \sum_{i=1}^n \text{log} f(Y_i|\hat{\boldsymbol{\theta}}_k)は n E \{ -2 \text{log} f(Y|\hat{\boldsymbol{\theta}}_k) \}の自然な推定量である．

最終的にn個の観測おける最大対数尤度 \sum_{i=1}^{n} \text{log} f(y_i|\hat{\boldsymbol{\theta}}_k)を使用した近似を行うため，ここからはn倍した期待カルバック不一致 E\{ nE\{ -2 \text{log} f(Y|\hat{\boldsymbol{\theta}}_k) \} \} = n \Delta(k)を近似することを考える．

以降の記述では簡潔さのため，kの下付き文字を省略する．

まず，真の分布 g(y)がパラメトリックなクラス \mathcal{F}(k)に含まれているという強い仮定を置く．この仮定の下で，真のパラメータを\boldsymbol{\theta}_0とすると，g(y)はf(y|\boldsymbol{\theta}_0)という形式で表現できる．また，最尤推定量\hat{\boldsymbol{\theta}}の漸近正規性と一致性を保証する正則条件も満たされているものと仮定する．

次にn\Delta(k)の等価な次の変形を考える．

\displaystyle \begin{align} n\Delta(k) &= n E \{ d (\hat{\boldsymbol{\theta}}) \} \\ &= E \{ -2 \text{log} f(\boldsymbol{Y}_n | \hat{\boldsymbol{\theta}}) \} \\ &~~~~ + [E \{ -2 \text{log} f(\boldsymbol{Y}_n|\boldsymbol{\theta}_0) \} - E \{ -2 \text{log} f(\boldsymbol{Y}_n|\hat{\boldsymbol{\theta}}) \} ] \cdots (\alpha) \\ &~~~~ + [n E \{ d (\hat{\boldsymbol{\theta}}) \} - E \{ -2 \text{log} f(\boldsymbol{Y}_n|\boldsymbol{\theta}_0) \} ] ~ \cdots \cdots \cdots (\beta) \end{align}


ここで\text{log}f(\boldsymbol{Y}_n|\boldsymbol{\theta})=\text{log}\{\prod_{i=1}^n f(Y_i|\boldsymbol{\theta}) \}=\sum_{i=1}^n \text{log} f(Y_i|\boldsymbol{\theta})である．
また上の式の E\{ -2 \text{log} f(\boldsymbol{Y}_n|\boldsymbol{\theta}_0) \}は次のように n E \{ -2 \text{log} f(Y|\boldsymbol{\theta}_0) \}となることに留意する．この関係は後で使用する．余談だがこの関係は定数と考えられる\boldsymbol{\theta}_0の代わりに確率変数である\hat{\boldsymbol{\theta}}を使用した場合には当然成り立たない(自戒)

\displaystyle \begin{align} E\{ -2 \text{log} f(\boldsymbol{Y}_n|\boldsymbol{\theta}_0) \} &= E \left\{ \sum_{i=1}^n \{ -2 \text{log} f(Y_i|\boldsymbol{\theta}_0) \} \right\} = \sum_{i=1}^n E \{ -2 \text{log} f(Y_i|\boldsymbol{\theta}_0) \} \\ &= \sum_{i=1}^n E \{ -2 \text{log} f(Y|\boldsymbol{\theta}_0) \} = n E \{ -2 \text{log} f(Y|\boldsymbol{\theta}_0) \} \end{align}


ここから(\alpha)と(\beta)を求める．


(\alpha)に関して，E \{ -2 \text{log} f(\boldsymbol{Y}_n|\boldsymbol{\theta}_0) \}を近似的に求めるために，-2\text{log}f(\boldsymbol{Y}_n|\boldsymbol{\theta}_0)を\hat{\boldsymbol{\theta}}まわりで2次までのテイラ展開を行い，その結果の期待値を取る手順を踏む．

\displaystyle -2 \text{log} f(\boldsymbol{Y}_n|\boldsymbol{\theta}_0) \\ ~~~~~~~~ \approx -2 \text{log} f(\boldsymbol{Y}_n|\hat{\boldsymbol{\theta}}) -2 ( \boldsymbol{\theta}_0 - \hat{\boldsymbol{\theta}})^T \frac{\partial \text{log} f(\boldsymbol{Y}_n|\boldsymbol{\theta})}{\partial \boldsymbol{\theta} } \Biggr|_{\boldsymbol{\theta} = \hat{\boldsymbol{\theta}} } - {(\boldsymbol{\theta}_0 - \hat{\boldsymbol{\theta}})}^T \frac{ {\partial}^2 \text{log} f(\boldsymbol{Y}_n|\boldsymbol{\theta}) }{ \partial \boldsymbol{\theta} \partial \boldsymbol{\theta}^T } \Biggr|_{\boldsymbol{\theta} = \hat{\boldsymbol{\theta}} } ( \boldsymbol{\theta}_0 - \hat{\boldsymbol{\theta}})

対数尤度の微分は最尤推定量の点で0になるため1次の項は無視できる．
Divergence: from 0.571024% to 1.130209%

\displaystyle \begin{align} -2 \text{log} f(\boldsymbol{Y}_n|\boldsymbol{\theta}_0) &{\approx} -2 \text{log} f(\boldsymbol{Y}_n|\hat{\boldsymbol{\theta}}) - {(\boldsymbol{\theta}_0 - \hat{\boldsymbol{\theta}})}^T \frac{ {\partial}^2 \text{log} f(\boldsymbol{Y}_n|\boldsymbol{\theta}) }{ \partial \boldsymbol{\theta} \partial \boldsymbol{\theta}^T } \Biggr|_{\boldsymbol{\theta} = \hat{\boldsymbol{\theta}}} ( \boldsymbol{\theta}_0 - \hat{\boldsymbol{\theta}}) \\ &= -2 \text{log} f(\boldsymbol{Y}_n|\hat{\boldsymbol{\theta}}) + {(\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0)}^T \left\{ - \frac{ {\partial}^2 \text{log} f(\boldsymbol{Y}_n|\boldsymbol{\theta}) }{ \partial \boldsymbol{\theta} \partial \boldsymbol{\theta}^T } \Biggr|_{\boldsymbol{\theta} = \hat{\boldsymbol{\theta}}} \right\} (\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0) \\ &= -2 \text{log} f(\boldsymbol{Y}_n|\hat{\boldsymbol{\theta}}) + {(\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0)}^T \mathcal{J}(\hat{\boldsymbol{\theta}}) (\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0) \end{align}

ここで\mathcal{J}(\boldsymbol{\theta})はObserved Fisher情報量である．
Observed/Expected Fisher情報量の違いや性質，また関連する漸近正規性の導出等はPawitan (2013)が詳しくわかり易い

期待値を取って次のようになる．

\displaystyle E \{ -2 \text{log} f(\boldsymbol{Y}_n|\boldsymbol{\theta}_0) \} \approx E \{ -2 \text{log} f(\boldsymbol{Y}_n|\hat{\boldsymbol{\theta}}) \} + E \{ {(\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0)}^T \mathcal{J}(\hat{\boldsymbol{\theta}}) (\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0) \}

上の式を(\alpha)のE \{ -2 \text{log} f(\boldsymbol{Y}_n|\boldsymbol{\theta}_0) \}に代入し，(\alpha)自体は次のようになる．

(\alpha) \approx E \{ {(\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0)}^T \mathcal{J}(\hat{\boldsymbol{\theta}}) (\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0) \}

ここで\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0は漸近的に多変量正規分布 N_k (\boldsymbol{0}, { \{ \mathcal{J}(\hat{\boldsymbol{\theta}}) \} }^{-1})に従い(Madisen and Thyregod (2010), p.22, (2.38))，(\alpha)の期待値内は {\chi}^2 (k)分布に従う；ゆえに(\alpha)は次のようになる．

\displaystyle (\alpha) \approx E \{ {(\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0)}^T \mathcal{J}(\hat{\boldsymbol{\theta}}) (\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0) \} = k


次に(\beta)に関しても，(\alpha)と類似し，n E \{ d (\hat{\boldsymbol{\theta}}) \}を近似的に求めるために，d(\hat{\boldsymbol{\theta}})を\boldsymbol{\theta}_0まわりで2次までのテイラ展開を行い，その結果にnを乗じて期待値を取るという手順を踏む．

\displaystyle d(\hat{\boldsymbol{\theta}}) \approx d(\boldsymbol{\theta}_0) + (\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0)^T \frac{ \partial d(\boldsymbol{\theta}) }{ \partial \boldsymbol{\theta} } \Biggr|_{\boldsymbol{\theta} = \boldsymbol{\theta}_0 } + \frac{1}{2} { (\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0) }^T \frac{ {\partial}^2 d (\boldsymbol{\theta}) }{ \partial \boldsymbol{\theta} \partial \boldsymbol{\theta}^T } \Biggr|_{\boldsymbol{\theta} = \boldsymbol{\theta}_0 } (\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0)

次のように1次の項は0になる(微分と積分の順序交換は無邪気にできると仮定する)．

\displaystyle \begin{align} \frac{ \partial d (\boldsymbol{\theta}) }{ \partial \boldsymbol{\theta} } \Biggr|_{\boldsymbol{\theta} = \boldsymbol{\theta}_0 } &= \frac{ \partial E \{ -2 \text{log} f(Y|\boldsymbol{\theta}) \} }{ \partial \boldsymbol{\theta} } \Biggr|_{\boldsymbol{\theta} = \boldsymbol{\theta}_0 } = -2 \frac{ \partial }{ \partial \boldsymbol{\theta} } \int g(y) \text{log} f(y|\boldsymbol{\theta}) \text{dy} \Biggr|_{\boldsymbol{\theta} = \boldsymbol{\theta}_0 } \\ &= -2 \int \frac{ g(y) }{ f(y| \boldsymbol{\theta}_0 ) } \frac{ \partial f(y| \boldsymbol{\theta}) }{ \partial \boldsymbol{\theta} } \Biggr|_{\boldsymbol{\theta} = \boldsymbol{\theta}_0 } \text{dy} = -2 \frac{ \partial }{ \partial \boldsymbol{\theta} } \int f(y|\boldsymbol{\theta}) \text{dy} \Biggr|_{\boldsymbol{\theta} = \boldsymbol{\theta}_0 } = \boldsymbol{0} \end{align}

したがってd(\hat{\boldsymbol{\theta}})は次のようになる．

\displaystyle \begin{align} d(\hat{\boldsymbol{\theta}}) &{\approx} E \{ -2 \text{log} f(Y | \boldsymbol{\theta}_0) \} + (\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0 )^T E \left\{ - \frac{ {\partial}^2 \text{log} f(Y | \boldsymbol{\theta}) }{ \partial \boldsymbol{\theta} \partial \boldsymbol{\theta}^T } \Biggr|_{\boldsymbol{\theta} = \boldsymbol{\theta}_0 } \right\} (\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0 ) \\ &= E \{ -2 \text{log} f(Y | \boldsymbol{\theta}_0) \} + (\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0)^T \mathcal{I}_1 (\boldsymbol{\theta}_0 ) (\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0) \end{align}

ここで\mathcal{I}_1 (\boldsymbol{\theta})は1個の観測に関するExpected Fisher情報量である．

期待値を取って次のようになる．ここで二重の期待値の外側がg(\boldsymbol{y}_n)に関するものであったことに注意すると E\{E \{ -2 \text{log} f(y | \boldsymbol{\theta}_0) \}\}=E \{ -2 \text{log} f(y | \boldsymbol{\theta}_0) \}である．

\displaystyle \begin{align} n E \{ d(\hat{\boldsymbol{\theta}}) \} &{\approx} n E \{ -2 \text{log} f(Y | \boldsymbol{\theta}_0) \} + n E \{ (\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0)^T \mathcal{I}_1 (\boldsymbol{\theta}_0 ) (\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0) \} \\ &= n E \{ -2 \text{log} f(Y | \boldsymbol{\theta}_0) \} + E \{ (\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0)^T \mathcal{I} (\boldsymbol{\theta}_0 ) (\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0) \} \end{align}

ここで\mathcal{I} (\boldsymbol{\theta}_0 )はn個の観測に関するExpected Fisher情報量である．Expected Fisher情報量の性質としてn \mathcal{I}_1 (\boldsymbol{\theta}_0 ) = \mathcal{I} (\boldsymbol{\theta}_0 )である．
上の式を(\beta)のn E \{ d (\hat{\boldsymbol{\theta}} ) \}に代入し， E\{ -2 \text{log} f(\boldsymbol{Y}_n|\boldsymbol{\theta}_0) \} = n E \{ -2 \text{log} f(Y|\boldsymbol{\theta}_0) \}であったことに注意すると，(\beta)自体は次のようになる．

\displaystyle (\beta) \approx E \{ (\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0)^T \mathcal{I} (\boldsymbol{\theta}_0 ) (\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0) \}

(\beta)の場合においても，\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0は漸近的に多変量正規分布 N_k (\boldsymbol{0}, {\{\mathcal{I} (\boldsymbol{\theta}_0) \}}^{-1}) に従い(Madisen and Thyregod (2010), p.22, (2.37))，(\beta)の期待値内は {\chi}^2 (k)分布に従う．ゆえに(\beta)は次のようになる．

\displaystyle (\beta) \approx E \{ (\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0)^T \mathcal{I} (\boldsymbol{\theta}_0 ) (\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0) \} = k



(\alpha)と(\beta)に関して得られた結果をまとめると漸近的に次のようになる．

n\Delta(k) = n E \{ d (\hat{\boldsymbol{\theta}}) \} \approx E \{ -2 \text{log} f (\boldsymbol{Y}_n|\hat{\boldsymbol{\theta}}) \} + 2k

ここから最終的に赤池情報量規準は次のように定義される．

\displaystyle \text{AIC} = -2 \sum_{i=1}^n \text{log} f(y_i | \hat{\boldsymbol{\theta}}) + 2k

\text{AIC}の期待値は漸近的にn倍した期待カルバック不一致を近似する．

E \{ \text{AIC} \} = E\{-2 \text{log} f(\boldsymbol{Y}_n | \hat{\boldsymbol{\theta}})\} + 2k \approx n \Delta(k)





Divergence: from 1.130209% to 0.571024%
上から分岐．以下の議論は自信がない．単なる怪聞になっているかも知れない．
対数尤度の微分は最尤推定量の点で0になるため1次の項は無視できる．
また，最尤推定量の仮定された一致性からn \rightarrow \inftyで\hat{\boldsymbol{\theta}}は\boldsymbol{\theta}_0へ確率収束するため，複数の確率収束する確率変数の四則演算に関する保存性と連続写像定理を考慮すると(こことここを参照)，ここでの近似の誤差が任意の実数\epsilon > 0より大きくなる確率は0に収束する．

\displaystyle \lim_{n \rightarrow \infty} P \left\{\left| -2 \text{log} f(\boldsymbol{Y}_n|\boldsymbol{\theta}_0) - \left\{ -2 \text{log} f(\boldsymbol{Y}_n|\hat{\boldsymbol{\theta}}) - {(\boldsymbol{\theta}_0 - \hat{\boldsymbol{\theta}})}^T \frac{ {\partial}^2 \text{log} f(\boldsymbol{Y}_n|\boldsymbol{\theta}) }{ \partial \boldsymbol{\theta} \partial \boldsymbol{\theta}^T } \Biggr|_{\boldsymbol{\theta} = \hat{\boldsymbol{\theta}} } (\boldsymbol{\theta}_0 - \hat{\boldsymbol{\theta}}) \right\}\right| > \epsilon \right\} = 0

このことを確率的ランダウの記号を用いて表示すればo_p(1)となる．最尤推定量は確率変数なので通常の極限的にo(1)のような近似誤差の評価できないと考えられる；この点を考慮して最尤推定量の一致性を利用するならo_p(1)になるはずである．

\displaystyle \begin{align} -2 \text{log} f(\boldsymbol{Y}_n|\boldsymbol{\theta}_0) &= -2 \text{log} f(\boldsymbol{Y}_n|\hat{\boldsymbol{\theta}}) - {(\boldsymbol{\theta}_0 - \hat{\boldsymbol{\theta}})}^T \frac{ {\partial}^2 \text{log} f(\boldsymbol{Y}_n|\boldsymbol{\theta}) }{ \partial \boldsymbol{\theta} \partial \boldsymbol{\theta}^T } \Biggr|_{\boldsymbol{\theta} = \hat{\boldsymbol{\theta}} } (\boldsymbol{\theta}_0 - \hat{\boldsymbol{\theta}}) + o_p(1) \\ &= -2 \text{log} f(\boldsymbol{Y}_n|\hat{\boldsymbol{\theta}}) + {(\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0)}^T \left\{ - \frac{ {\partial}^2 \text{log} f(\boldsymbol{Y}_n|\boldsymbol{\theta}) }{ \partial \boldsymbol{\theta} \partial \boldsymbol{\theta}^T } \Biggr|_{\boldsymbol{\theta} = \hat{\boldsymbol{\theta}} } \right\} (\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0) + o_p(1) \\ &= -2 \text{log} f(\boldsymbol{Y}_n|\hat{\boldsymbol{\theta}}) + {(\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0)}^T \mathcal{J}(\hat{\boldsymbol{\theta}}) (\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0) + o_p(1) \end{align}

上述のように確率収束する近似誤差を考慮に入れて展開を進め，追加で一様可積分性のような正則条件が満たされていると仮定するとE\{o_p(1)\} =o(1)となり(こことここを参照；なにか公式なソースではないので確証はないが...)，最終的に期待カルバック不一致は次のようになる．

n\Delta(k) = n E \{ d (\hat{\boldsymbol{\theta}}) \} = E \{ -2 \text{log} f (\boldsymbol{Y}_n|\hat{\boldsymbol{\theta}}) \} + 2k + o(1)

ここから赤池情報量規準は次のように定義される．

\displaystyle \text{AIC} = -2 \sum_{i=1}^n \text{log} f(y_i | \hat{\boldsymbol{\theta}}) + 2k

ここで\text{AIC}の期待値はn \rightarrow \inftyで0になる誤差を伴ってn \Delta(k)を近似する．

E \{ \text{AIC} \} + o(1) = n \Delta(k)



所感

本編導出では，Cavanaugh and Neath (2018)に頻出する記号であるyが，ベクタ(複数の観測)なのかスカラ(1つの観測)なのか，確率変数なのか実現値なのか，どこまでの文脈の範囲で同じで，また違うのか正直良くわからなかったため，全体の方向性は踏襲しつつも，カルバックライブラ情報量の期待値における変数は1変量の確率変数にすることを主軸とし，直感に適うことを優先しながら曖昧な点を順次確定する形で導出を行った．
Cavanaugh and Neath (2018)と最終的な形は異なるが，少なくともyを一貫してベクタとして捉えると等価になる気がする(ぱっとした想像だけで厳密に検証はしてないが；ただしこの場合カルバックライブラ情報量の期待値の変数もベクタになり，個人的に解釈が難しい)；一貫してスカラの場合，多分難しそうなのと，今の自分の知識の範囲ではObserved Fisher情報量とExpected Fisher情報量あたりで突っかかりそうな気がする．

またCavanaugh and Neath (2018)の導出ではテイラ展開の誤差の評価としてo(1)が現れている．調べてみたものの自信がないので，本編導出では全て近似で乗り切ったところであるが(Divergence: 0.571024%)，一応o(1)が現れる道筋はつかめている(Divergence: 1.130209%)．この点については厳密に確証を得ようと考えると中々難易度が高そうである；測度論的確率論がわからないので，その基礎からはじめて半年～１年程度は要しそうである．まったくもって自明で無いように見えるのに，なぜCavanaugh and Neath (2018)には別段の説明もなく，さらっとo(1)が登場しているのかは本当に疑問である．ただ自分が遠回りしているだけで，なにか簡潔に進める未知の前提がどこかにあるのかも知れない．んーとても口惜しい．途中の世界線変動率には特に意味はない．ラ・ヨダソウ・スティアーナ


ベイズ情報量規準と修正付き赤池情報量規準を経由して，ようやく赤池情報量規準の導出を一通り追ったが，漸近正規性関連＋ExpectedとObserved Fisher情報量まわりでも大変混乱した．これらはいくつかの点で，証明なしにテキストに載っていることをそのまま信じる形で導出を進めたが，いまだ拭えない不安が残っている．現状時間が足りないが，いつかこれらもしっかり基礎から学習して不安を払拭したい．手近でHeld and Bové (2014)にこの辺りがざっくり載ってることに気がついた．まぁ近いうちに


\text{AIC}の導出途中で狐につままれたような\Delta(k)と等価な変形を行ったが，Konishi and Kitagawa (2008)のFig. 3.7で図示されるような期待対数尤度と対数尤度間で生じるバイアスの分解と類似のものな気がする．ちゃんと対応をとって見てないのではっきりとは言えないが．

Konishi and Kitagawa (2008)と言えば，この本に載っているAICcの導出は，明確にテイラ展開や漸近正規性を用いないと書かれているサブセクション(3.5.1)に基づいているが，式(7.65)から(7.66)の変形では暗に最尤推定量の漸近正規性を利用しているように見える．あるいはE_G[(X\boldsymbol{\beta}_0 - X\hat{\boldsymbol{\beta}})^T(X\boldsymbol{\beta}_0 - X\hat{\boldsymbol{\beta}})/(n \hat{\sigma}^2)]を漸近正規性を用いずに求める方法があるのだろうか？今の自分にはわからない Madisen and Thyregod (2010)のTheorem 3.3に記載されてるように一般線形モデル(正規線形モデル)においては，誤差に仮定された正規性から直接的に回帰係数の推定量が正規分布に従うことが求められるので，ここでの疑問点は解消した．


今回も例にもれず，改善点・間違い等は見つかり次第修正する．

修正済み赤池情報量規準(AICc)の導出

Hurvich and Tsai (1989)を流し読みして得た理解まとめ

準備

まず，データは次のTrue Modelから生成されたと仮定する．

\boldsymbol{y} = \boldsymbol{\mu} + \boldsymbol{\epsilon}
\text{where}
~~~~ \boldsymbol{y} = (y_1, \cdots, y_n)^T,
~~~~ \boldsymbol{\mu} = ({\mu}_1, \cdots, {\mu}_n)^T,
~~~~ \boldsymbol{\epsilon} = ({\epsilon}_1, \cdots, {\epsilon}_n)^T, {\epsilon}_i \overset{\text{i.i.d.}}{\sim} N(0, {{\sigma}_0}^2).

Hurvich and Tsai (1989)ではTrue Modelの意味でOperating Modelという用語が使われているが，どういうニュアンスを含んでいるのかよくわからない

また，近似に用いるモデル族として次のものを考える．

\boldsymbol{y} = \boldsymbol{h}(\boldsymbol{\theta}) + \boldsymbol{u}
\text{where}
~~~~ \boldsymbol{h}(\boldsymbol{\theta}) = (h_1(\boldsymbol{\theta}), \cdots, h_n(\boldsymbol{\theta}))^T.
~~~~ \boldsymbol{u} = (u_1, \cdots, u_n)^T, u_i \overset{\text{i.i.d.}}{\sim} N(0, {\sigma}^2)

\boldsymbol{\theta}はm次元ベクタ，\boldsymbol{h}は連続で2階微分可能であると仮定する．

近似に用いるモデルとTrue Modelの具体例として，両者が線形モデルであるとすると，\boldsymbol{h}(\boldsymbol{\theta})=X\boldsymbol{\theta}，\boldsymbol{\mu}=X_0\boldsymbol{\theta}_0となる．ここでXとX_0は各々にn \times mとn \times m_0のフルランクの行列，\boldsymbol{\theta}_0はm_0次元ベクタである．


近似に用いるモデルとTrue Modelの乖離を測る有用な指標として，カルバック・ライブラ情報量がある．

\Delta(\boldsymbol{\theta}, {\sigma}^2) = E_F\{ -2 \text{log} (g_{\boldsymbol{\theta},{\sigma}^2}(\boldsymbol{y})) \}

ここでFは期待値がTrue Modelに関するものであることを示し，g_{\boldsymbol{\theta},{\sigma}^2}(\boldsymbol{y})は近似に用いるモデルに基づいた尤度関数である．ここでのカルバック・ライブラ情報量は定数になる項を無視し，2をかけている．

カルバック・ライブラ情報量が小さいほど，対象となったモデルとTrue Modelの乖離が少ない．


正規分布についての尤度関数を次に示す．

\displaystyle \begin{align} g_{\boldsymbol{\theta},{\sigma}^2}(\boldsymbol{y}) &= \prod_{i=1}^n \left\{ (2 \pi {\sigma}^2)^{-\frac{1}{2}} \text{exp} \left\{ -\frac{(y_i-h_i(\boldsymbol{\theta}))^2}{2 {\sigma}^2 } \right\} \right\} \\ &= (2 \pi {\sigma}^2)^{-\frac{n}{2}} \text{exp} \left\{ -\frac{1}{2{\sigma}^2} \sum_{i=1}^n (y_i - h_i (\boldsymbol{\theta}))^2 \right\} \\ &= (2 \pi {\sigma}^2)^{-\frac{n}{2}} \text{exp} \left\{ -\frac{(\boldsymbol{y} - \boldsymbol{h}(\boldsymbol{\theta}))^T(\boldsymbol{y} - \boldsymbol{h}(\boldsymbol{\theta}))}{2 {\sigma}^2} \right\} \end{align}

具体的に得られた尤度関数からカルバック・ライブラ情報量は次のようになる．

\displaystyle \begin{align} \Delta (\boldsymbol{\theta}, {\sigma}^2) &= -2 E_F \left[ \text{log} \left\{ (2 \pi {\sigma}^2)^{-\frac{n}{2}} \text{exp} \left\{ -\frac{(\boldsymbol{y} - \boldsymbol{h}(\boldsymbol{\theta}))^T(\boldsymbol{y} - \boldsymbol{h}(\boldsymbol{\theta}))}{2 {\sigma}^2} \right\} \right\} \right] \\ &= n \text{log} (2 \pi {\sigma}^2) + \frac{1}{{\sigma}^2} E_F \left[ (\boldsymbol{\mu} + \boldsymbol{\epsilon} - \boldsymbol{h} (\boldsymbol{\theta}))^T(\boldsymbol{\mu} + \boldsymbol{\epsilon} - \boldsymbol{h} (\boldsymbol{\theta})) \right] \\ &= n \text{log} (2 \pi {\sigma}^2) + \frac{n {{\sigma}_0}^2}{{\sigma}^2} + \frac{(\boldsymbol{\mu} - \boldsymbol{h} (\boldsymbol{\theta}))^T(\boldsymbol{\mu} - \boldsymbol{h} (\boldsymbol{\theta}))}{{\sigma}^2} \end{align}


補足蛇足
\boldsymbol{\alpha} = \boldsymbol{\mu} - \boldsymbol{h}(\boldsymbol{\theta})
\displaystyle (\boldsymbol{\epsilon} - \boldsymbol{\alpha})^T(\boldsymbol{\epsilon} - \boldsymbol{\alpha}) = \sum_{i=1}^n ({\epsilon}_i + {\alpha}_i)^2 = \sum_{i=1}^n ({\epsilon}^2 +2 {\epsilon}_i \alpha + {{\alpha}_i}^2) = \sum_{i=1}^n {{\epsilon}_i}^2 + 2 \sum_{i=1}^n {\epsilon}_i {\alpha}_i + \sum_{i=1}^n {{\alpha}_i}^2
\displaystyle E\left[\sum_{i=1}^n {{\epsilon}_i}^2 \right] = n {{\sigma}_0}^2, ~~ E\left[2 \sum_{i=1}^n {\epsilon}_i {\alpha}_i \right] = 0, ~~ E\left[ \sum_{i=1}^n {{\alpha}_i}^2 \right] =(\boldsymbol{\mu} - \boldsymbol{h} (\boldsymbol{\theta}))^T(\boldsymbol{\mu} - \boldsymbol{h} (\boldsymbol{\theta}))


妥当な規準として近似に用いるモデルを評価するため，カルバック・ライブラ情報量の期待値 E_F \{ \Delta (\boldsymbol{\theta}, {\sigma}^2) \}を取り，パラメータとして得られたデータに基づいた最尤推定量(\hat{\boldsymbol{\theta}}, \hat{\sigma}^2)を使用する．

\displaystyle \hat{\boldsymbol{\theta}} = \underset{\boldsymbol{\theta}}{\text{argmin}} (\boldsymbol{\mu} - \boldsymbol{h} (\boldsymbol{\theta}))^T(\boldsymbol{\mu} - \boldsymbol{h} (\boldsymbol{\theta}))
\displaystyle \hat{\sigma}^2 = \frac{1}{n}(\boldsymbol{\mu} - \boldsymbol{h} (\hat{\boldsymbol{\theta}}))^T(\boldsymbol{\mu} - \boldsymbol{h} (\hat{\boldsymbol{\theta}}))

最尤推定量を適用してカルバック・ライブラ情報量は次のようになる．

\displaystyle \Delta (\hat{\boldsymbol{\theta}}, \hat{\sigma}^2) = n \text{log} (2 \pi \hat{\sigma}^2) + \frac{n {{\sigma}_0}^2}{\hat{\sigma}^2} + \frac{(\boldsymbol{\mu} - \boldsymbol{h} (\hat{\boldsymbol{\theta}}))^T(\boldsymbol{\mu} - \boldsymbol{h} (\hat{\boldsymbol{\theta}}))}{\hat{\sigma}^2}

Hurvich and Tsai (1989)では，この段階でn\text{log}(2 \pi)が定数として無視されるが理由は不明．n\text{log}(2 \pi)を無視すると尤度との関係がわかり難くなるので良いことはない気がするが…

近似に用いるモデル族が複数あるとき，E_F \{ \Delta (\hat{\boldsymbol{\theta}}, \hat{\sigma}^2) \}を最小化するものが，ある意味でTrue Modelに最も近いものとして選択され得る．

実際にはTrue Modelは未知であるから，それに基づくE_F \{ \Delta (\hat{\boldsymbol{\theta}}, \hat{\sigma}^2) \}も同様に未知である．しかし，何らかの追加の仮定が置かれることで，この量は推定され得る．推定され得る1例として，次に示す赤池情報量規準は近似的にE_F \{ \Delta (\hat{\boldsymbol{\theta}}, \hat{\sigma}^2) \}の不偏推定量を提供する．

AIC = n(\text{log} ( 2 \pi \hat{\sigma}^2) + 1) + 2 (m + 1)

ここでmは近似に用いるモデルのパラメータの次数である．また，n(\text{log} ( 2 \pi \hat{\sigma}^2)+1)は最大対数尤度l \times -2と等しい．


AICcの導出

ここでの目標は次のE_F \{ \Delta (\hat{\boldsymbol{\theta}}, \hat{\sigma}^2) \}の推定量を得ることであり，それが最終的にAICcを導く．

\displaystyle \begin{align} E_F \{ \Delta (\hat{\boldsymbol{\theta}}, \hat{\sigma}^2) \} &= E_F \left\{ n \text{log} (2 \pi \hat{\sigma}^2) + \frac{n {{\sigma}_0}^2}{\hat{\sigma}^2} + \frac{(\boldsymbol{\mu} - \boldsymbol{h} (\hat{\boldsymbol{\theta}}))^T(\boldsymbol{\mu} - \boldsymbol{h} (\hat{\boldsymbol{\theta}}))}{\hat{\sigma}^2} \right\} \\ &= E_F \left\{ n \text{log} (2 \pi \hat{\sigma}^2) \right\} + E_F \left\{ \frac{n {{\sigma}_0}^2 }{\hat{\sigma}^2} \right\} + E_F \left\{ \frac{(\boldsymbol{\mu} - \boldsymbol{h}(\hat{\boldsymbol{\theta}}))^T (\boldsymbol{\mu} - \boldsymbol{h}(\hat{\boldsymbol{\theta}}))}{\hat{\sigma}^2} \right\} \end{align}


まず，(SSE / {{\sigma}_0}^2) \sim {\chi}^2(n-m)を定理として受け入れ，\hat{\sigma}^2の定義よりSSE = n \hat{\sigma}^2であることから，n \hat{\sigma}^2 / {{\sigma}_0}^2は{\chi}^2(n-m)に従い，{{\sigma}_0}^2/(n \hat{\sigma}^2)は\text{Inv-}{\chi}^2(n-m)に従う．ここで証明なしに(SSE / {{\sigma}_0}^2) \sim {\chi}^2(n-m)を定理として受け入れたが，これは調べればWikiにも出てくる；自由度あたりが浅学過ぎて証明はわからない．書籍として少なくともPuntanen et al. (2013)には載ってる．
このことからE_F \{ \Delta (\hat{\boldsymbol{\theta}}, \hat{\sigma}^2) \}の右辺第2項は次のように求まる．

\displaystyle E_F \left\{ \frac{n {{\sigma}_0}^2}{\hat{\sigma}^2} \right\} = n^2 E_F \left\{ \frac{{{\sigma}_0}^2}{n \hat{\sigma}^2} \right\} = \frac{n^2}{n-m-2}


以下，近似に用いるモデル族にTrue Modelが含まれているという強い仮定を置く．この仮定の下でTrue Modelの平均応答\muは\mu = \boldsymbol{h} ( \boldsymbol{\theta}^{*} )となる．ここで\boldsymbol{\theta}^{*}はm \times 1次元の未知のベクタである．
次に，\boldsymbol{h} (\hat{\boldsymbol{\theta}}) の\boldsymbol{\theta} = \boldsymbol{\theta}^{*}におけるテイラ展開による1次近似を考える．

\boldsymbol{h} (\hat{\boldsymbol{\theta}}) \approx \boldsymbol{h} (\boldsymbol{\theta}^{*}) + V (\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}^{*})

ここでVは\hat{\boldsymbol{\theta}} = \boldsymbol{\theta}^{*}における\partial \boldsymbol{h} / \partial \boldsymbol{\theta}である．追加の仮定として線形モデルを考えるとVは計画行列になり，\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}^{*}は多変量正規分布N_m(\boldsymbol{0}, {{\sigma}_0}^2 (V^T V)^{-1})に従う(Madisen and Thyregod (2010), p.49, Theorem 3.3)．Hurvich and Tsai (1989)では\boldsymbol{h}を線形モデルに限定した書き方はしていないが，非線形モデルの場合でも同様の正規性が導入できるのかは浅学過ぎてよくわからない．

以上からE_F \{ \Delta (\hat{\boldsymbol{\theta}}, \hat{\sigma}^2) \}の右辺第3項の期待値内は近似的にF分布に帰着できる．

\displaystyle \begin{align} \frac{(\boldsymbol{\mu} - \boldsymbol{h}(\hat{\boldsymbol{\theta}}))^T (\boldsymbol{\mu} - \boldsymbol{h}(\hat{\boldsymbol{\theta}}))}{\hat{\sigma}^2} &= \frac{(\boldsymbol{h}(\boldsymbol{\theta}^{*}) - \boldsymbol{h}(\hat{\boldsymbol{\theta}}))^T (\boldsymbol{h}(\boldsymbol{\theta}^{*}) - \boldsymbol{h}(\hat{\boldsymbol{\theta}}))}{\hat{\sigma}^2} \\ &\approx \frac{ ( \hat{\boldsymbol{\theta}} - \boldsymbol{\theta}^{*})^T V^T V ( \hat{\boldsymbol{\theta}} - \boldsymbol{\theta}^{*} ) }{ \hat{\sigma}^2 } \\ &= \frac{nm}{n-m} \frac{ ( ( \hat{\boldsymbol{\theta}} - \boldsymbol{\theta}^{*})^T V^T V ( \hat{\boldsymbol{\theta}} - \boldsymbol{\theta}^{*} ) / {{\sigma}_0}^2 ) (1/m) }{ (n \hat{\sigma}^2 / {{\sigma}_0}^2) (1/(n-m)) } \end{align}


\displaystyle \Rightarrow \frac{n-m}{nm} \frac{(\boldsymbol{\mu} - \boldsymbol{h}(\hat{\boldsymbol{\theta}}))^T (\boldsymbol{\mu} - \boldsymbol{h}(\hat{\boldsymbol{\theta}}))}{\hat{\sigma}^2} \approx \frac{ ( ( \hat{\boldsymbol{\theta}} - \boldsymbol{\theta}^{*})^T V^T V ( \hat{\boldsymbol{\theta}} - \boldsymbol{\theta}^{*} ) / {{\sigma}_0}^2 ) (1/m) }{ (n \hat{\sigma}^2 / {{\sigma}_0}^2) (1/(n-m)) } \sim F(m, n-m)

ゆえに

\displaystyle \begin{align} E_F \left\{ \frac{ (\boldsymbol{\mu} - \boldsymbol{h}( \hat{\boldsymbol{\theta}} ) )^T (\boldsymbol{\mu} - \boldsymbol{h}( \hat{\boldsymbol{\theta}} ) ) }{\hat{\sigma}^2} \right\} &= \frac{nm}{n-m} E_F \left\{ \frac{n-m}{nm} \frac{ (\boldsymbol{\mu} - \boldsymbol{h}( \hat{\boldsymbol{\theta}} ) )^T (\boldsymbol{\mu} - \boldsymbol{h}( \hat{\boldsymbol{\theta}} ) ) }{\hat{\sigma}^2} \right\} \\ &{ \approx ~} \frac{nm}{n-m} E_F \left\{ \frac{ ( ( \hat{\boldsymbol{\theta}} - \boldsymbol{\theta}^{*})^T V^T V ( \hat{\boldsymbol{\theta}} - \boldsymbol{\theta}^{*} ) / {{\sigma}_0}^2 ) (1/m) }{ (n \hat{\sigma}^2 / {{\sigma}_0}^2) (1/(n-m)) } \right\} \\ &= \frac{nm}{n-m} \frac{n-m}{n-m-2} = \frac{nm}{n - m - 2} \end{align}


最終的に全体としてまとめるとE_F \{ \Delta (\hat{\boldsymbol{\theta}}, \hat{\sigma}^2) \}は次のようになる．

\displaystyle \begin{align} E_F \{ \Delta (\hat{\boldsymbol{\theta}}, \hat{\sigma}^2) \} ~ &{\approx} ~ E_F \{ n \text{log} (2 \pi \hat{\sigma}^2) \} + \frac{n^2}{n-m-2} + \frac{nm}{n - m - 2} \\ &= E_F \{ n ( \text{log} (2 \pi \hat{\sigma}^2) + 1) \} + \frac{2 n (m + 1) }{n - m - 2} \end{align}

そしてここからAICcは次のように定義される．

\displaystyle \text{AICc} = n ( \text{log} (2 \pi \hat{\sigma}^2) + 1) + \frac{2 n (m + 1) }{n - m - 2} = \text{AIC} + \frac{2 (m + 1) (m + 2) }{n - m - 2}

AICcの期待値はE_F \{ \Delta (\hat{\boldsymbol{\theta}}, \hat{\sigma}^2) \}を近似する．

\displaystyle E_F \{ \text{AICc} \} = E_F \{ n ( \text{log} (2 \pi \hat{\sigma}^2) + 1) \} + \frac{2 n (m + 1) }{n - m - 2} \approx E_F \{ \Delta (\hat{\boldsymbol{\theta}}, \hat{\sigma}^2) \}


上のAICcの罰則項は少し見慣れないかもしれないが，正規線形モデル等で推定される分散もはじめから考慮に入れたパラメータ数としてk=m+1とすれば，比較的よく見かけるAICcになる．

\displaystyle \text{AICc} = n (\text{log} (2 \pi \hat{\sigma}^2) + 1) + \frac{2 n k}{n - k - 1} = \text{AIC} + \frac{2 k (k + 1) }{n - k - 1}




前のBlogでAICcの利用法に関して，情報量規準で意図される罰則項という観点から述べたが，AICcの導出過程から罰則項の分母は\text{Inv-}{\chi}^2分布とF分布の自由度に由来するものであるため，明確にn>m+1とならない場合の使用は悪用である．


今回も思いの外長くなった．Hurvich and Tsai (1989)を読んでざっくりは理解できた気がしていたが，これを書いてて理解の穴が多分にあることに気がついた．さらなる研鑽が必要である(小並感)．なにか改善点・間違いに気がついたら修正する．

ベイズ情報量規準の導出のスケッチ

下記の文献のBICのところを流し読みして得た理解まとめ
link.springer.com

事後確率に基づくモデル選択

M_1,M_2,\cdots,M_rをr個の候補モデルとし，各モデルM_iは確率分布f_i(x| \boldsymbol{ \theta }_i ) (\boldsymbol{\theta}_i \in {\Theta}_i \subset \mathbb{R}^{k_i})とk_i次元パラメータベクタ\boldsymbol{\theta}_iを取る事前分布{\pi}_i (\boldsymbol{\theta}_i)に特徴づけられるものとする．

ここでのモデルとは，回帰モデルにおいて説明変数を何個含むか，あるいはどのような分布が仮定されるかというような構造レベルのものである．

 
n個の標本\boldsymbol{x}_n = \{ x_1,\cdots,x_n\}があるとき，i番目のモデルM_iに関して周辺分布あるいは\boldsymbol{x_n}の確率は次のように与えられる．

\displaystyle p_i (\boldsymbol{x}_n) = \int f_i (\boldsymbol{x}_n|\boldsymbol{\theta}_i) {\pi}_i(\boldsymbol{\theta}_i)d\boldsymbol{\theta}_i
 

p_i (\boldsymbol{x}_n)はi番目のモデルM_iの尤度と考えられる．またp_i (\boldsymbol{x}_n)は，このモデルで具体的なパラメータ推定をベイズ的に行う際の周辺尤度になっている．

 
P(M_i)をi番目のモデルの事前確率とすると，ベイズの定理に基づき，i番目のモデルの事後確率は次のように与えられる．

\displaystyle P(M_i|\boldsymbol{x}_n)=\frac{p_i(\boldsymbol{x}_n)P(M_i)}{\sum^{r}_{j=1}p_j(\boldsymbol{x}_n)P(M_j)}
 

この事後確率は，データ\boldsymbol{x}_nが観察されたとき，i番目のモデルからそのデータが生成された確率を表しており，r個の候補モデルから1つのモデルを選択する状況では，この事後確率が最も大きいモデルを採用するが自然と考えられる．

P(M_i|\boldsymbol{x}_n)において，分母は全てのモデルで同一なので分子p_i(\boldsymbol{x}_n)P(M_i)のみを比較すれば良い；加えて事前確率P(M_i)が全てのモデルで同一と仮定すれば，モデルの尤度p_i(\boldsymbol{x}_n)のみの比較で事後確率の観点から最良のモデルが選択できる． 

P(M_i|\boldsymbol{x}_n)\propto p_i(\boldsymbol{x}_n)P(M_i) \propto p_i(\boldsymbol{x}_n)
 

ベイズ情報量規準の導出

事後確率P(M_i|\boldsymbol{x}_n)に基づく先に説明した方針のモデル選択を実現するために，p_i(\boldsymbol{x}_n)の近似としてベイズ情報量規準は導出される．具体的な形は次のようになる．

\displaystyle \begin{align} -2 \text{log} p_i(\boldsymbol{x}_n) &= -2 \text{log} \left\{ \int f_i (\boldsymbol{x}_n|\boldsymbol{\theta}_i) {\pi}_i (\boldsymbol{\theta}_i) d\boldsymbol{\theta}_i \right\} \\ &\approx -2 \text{log} f_i(\boldsymbol{x}_n|\hat{\boldsymbol{\theta}_i}) + k_i \text{log} (n) \end{align}
 
-2が付いたので，この量の小さいモデルが事後確率の大きいモデルに対応する．

以下の導出過程は上の書籍のものとは異る．間違いが含まれているかも

p_i(\boldsymbol{x}_n)の近似は，nが十分に大きいときに成り立つラプラス近似によって得られる．ラプラス近似は次のようなものである（今回はスケッチなのでラプラス近似は所与のものとして受け入れる）．

\displaystyle \int \text{exp}\{nq(\boldsymbol{\theta})\} d\boldsymbol{\theta} \approx \frac{(2\pi)^{p/2}}{n^{p/2}|J_q(\hat{\boldsymbol{\theta}})|^{1/2}}\text{exp}\{nq(\hat{\boldsymbol{\theta}})\},
 
\displaystyle \text{where  } J_q(\boldsymbol{\hat{\theta}}) = \left. - \frac{\partial^2 q(\boldsymbol{\theta})}{\partial \boldsymbol{\theta} \partial \boldsymbol{\theta}^T}\right|_{\boldsymbol{\theta}=\hat{\boldsymbol{\theta}}}
 

ここでq(\boldsymbol{\theta})はp次元パラメタベクタ\boldsymbol{\theta}を取る実数値関数，\hat{\boldsymbol{\theta}}はq(\boldsymbol{\theta})の最頻値である．
 
まず，ラプラス近似が適用できるようにp_i(\boldsymbol{x}_n)を変形する．

\displaystyle \begin{align} p_i(\boldsymbol{x}_n)&=\int f_i(\boldsymbol{x}_n|\boldsymbol{\theta}_i) {\pi}_i (\boldsymbol{\theta}_i) d\boldsymbol{\theta}_i \\&=\int \text{exp} \left\{ n \left[ \frac{1}{n}(\text{log} f_i(\boldsymbol{x}_n|\boldsymbol{\theta}_i)+\text{log}{\pi}_i(\boldsymbol{\theta}_i) ) \right]\right\} d\boldsymbol{\theta}_i \\ &= \int \text{exp} \left\{n \eta(\boldsymbol{\theta}_i)\right\}d\boldsymbol{\theta}_i \end{align}
 
ここでは\eta(\boldsymbol{\theta}_i)=n^{-1}(\text{log} f_i(\boldsymbol{x}_n|\boldsymbol{\theta}_i)+\text{log}{\pi}_i(\boldsymbol{\theta}_i))とした．
そして次の近似を得る．


\displaystyle \int \text{exp} \left\{n\eta(\boldsymbol{\theta}_i)\right\}d\boldsymbol{\theta}_i \approx \frac{(2\pi)^{k_i/2}}{n^{k_i/2}|J_{\eta}(\hat{\boldsymbol{\theta}_i})|^{1/2}}\text{exp}\{n\eta(\hat{\boldsymbol{\theta}_i})\}


 事前分布{\pi}_i(\boldsymbol{\theta}_i)が無情報事前分布であると仮定すると，\eta(\boldsymbol{\theta}_i)の\boldsymbol{\theta}_iに関する大小関係は対数尤度\text{log} f_i(\boldsymbol{x}_n|\boldsymbol{\theta}_i)に一致する．ゆえに，ここで\hat{\boldsymbol{\theta}_i}は最尤推定量である．{\pi}_i(\boldsymbol{\theta}_i)が無情報事前分布であるという仮定は上の書籍にはないが，式(9.17)の近似で{\pi}_i(\boldsymbol{\theta}_i)のテイラ展開の第2項以降を無視するところから暗に想定されている気がする


\displaystyle p_i(\boldsymbol{x}_n) \approx \frac{(2\pi)^{k_i/2}}{n^{k_i/2}|J_{\eta}(\hat{\boldsymbol{\theta}_i})|^{1/2}}\text{exp}\{n\eta(\hat{\boldsymbol{\theta}_i})\}


両辺の対数を取って-2をかける．


\displaystyle \small -2 \text{log} p_i(\boldsymbol{x}_n) \approx -2 \text{log} f_i(\boldsymbol{x}_n|\hat{\boldsymbol{\theta}_i}) -2 \text{log} {\pi}_i(\hat{\boldsymbol{\theta}_i}) - k_i \text{log}(2 \pi) + k_i \text{log} (n) + \text{log}(|J_{\eta}(\hat{\boldsymbol{\theta}_i})|) \normalsize


標本サイズnに関してO(1)以下の小さいオーダの項を無視して，最終的にベイズ情報量規準を得る．


-2 \text{log} p_i(\boldsymbol{x}_n) \approx \text{BIC} = -2 \text{log} f_i(\boldsymbol{x}_n|\hat{\boldsymbol{\theta}_i}) + k_i \text{log} (n)


標本サイズnに関してO(1)以下の小さいオーダの項を無視する部分は，直感的にn\rightarrow\inftyのとき，nのない項は無視できるくらい小さくなるということだと思うが，オーダの個人的な理解が足りてない





AICの導出に比べたら全然長くなさそうだから書き始めたが，思いほか長くなった．疲れた．途中ラプラス近似の適用の部分に不安があったが，確認したところ形式的には問題はなさそう．他になにか間違いがあったら，わかり次第修正する．

標本数とパラメータ数が近いときのAICcの挙動

検証用のシミュレーションを書いたり，調べ物をしてて，AIC_cについて気がついたことあったのでメモ．

 

AIC_cとは

AIC_cとは，モデル選択に用いられる情報量規準の1つであり，標本数nが漸近的に無限に大きくなることを仮定したAICを，有限のnに修正したものである．

AIC_c = -2l + \frac{2pn}{n-p-1} = AIC + \frac{2p(p+1)}{n-p-1}

 

ここでlは対象となるモデルの最大対数尤度，pはパラメータ数である．

直感的にn/pが小さいとき（ただしn\gt p+1），AIC_cにはAICよりも強い罰則が加わり，n/pが大きくなるに従ってAICに近づく．

n=p\,\,のときのAIC_c

標本数nとパラメータ数pが同じとき，AIC_cの罰則項は負になり，むしろ報酬項になり得る．

\frac{2pn}{n-p-1}\lt 0 \,\,\, if \,\,\, n = p

 

この性質から，AIC_cでモデル選択をする場合で，候補モデル中の最大パラメータ数p_{max}と標本数nが同じとき，その最大パラメータ数の候補モデルM(p_{max})は最も当てはまりが良く，加えてM(p_{max})に関してのみ罰則項が報酬項になるため，必ずそのM(p_{max})が選択される．

より広くn\leq pのとき，AIC_cの罰則項は報酬項になっているが，例えば線形回帰モデルであれば，n \lt pの計画行列Xでは(X^t X)^{-1}が求まらなそうなのであんまり意味はなさそう（線形代数力が足りなくて一般に証明は思いつかないが，n\lt pのとき，(X^t X)^{-1}は正則ではないと思う）．

n=p+1\,\,のときのAIC_c

 標本数nがパラメータ数p+1と同じとき，AIC_cはゼロ除算になるため，基本的に定義できない．

R言語など，ゼロ除算がa\gt 0,a/0=\inftyと定義されている言語でAIC_cを実装してモデル選択をする場合，例外でプログラムが止まることはないが，n=p_{max}+1\,\,となる候補モデル中の最大パラメータ数のモデルはAIC_cが無限になるため，決して選ばれなくなる．

 AIC_cの使用について

一般に情報量規準が罰則項で意図しているモデル選択上のparsimonyは，AIC_cにおいてn\leq p+1で成り立たない（実装によっては最悪例外が飛ぶ）．なのでAIC_cはn\gt p + 1での使用が推奨されると思う．

 n\leq p+1でAIC_cを使用した実例

journals.plos.org

先に説明したn\leq p+1におけるAIC_cの挙動は式を見ればすぐ気がつくことができるものである．だが上の論文ではプロットのみから挙動を論じたため，この点について解釈間違いをしているようである．結論とは関わりのない些細な部分ではあるので大筋に影響はないが．